Perceptron(퍼셉트론)

1. 수학적 정의

입력 신호 → 수상 돌기 → 축삭 돌기 → 출력 신호

수상 돌기에 여러 신호가 도착하면 세포체에 합쳐진다. 합쳐진 신호가 특정 임계값을 넘으면 출력 신호가 생성되고 축삭 돌기를 이용하여 전달된다. 로젠블라트(Frank Rosenblatt)는 뉴런 모델을 기반으로 퍼셉트론 학습 개념을 처음 발표했다. 퍼셉트론 규칙에서 로젠블라트는 자동으로 최적의 가중치를 학습하는 알고리즘을 제안했다. 이는 두 개의 클래스가 있는 이진분류 작업으로 볼 수 있다. 두 클래스는 간단하게 1(양성 클래스)과 -1(음성 클래스)로 나타낸다. 그 다음 입력 값 $\bf{x}$와 이에 상응하는 가중치 벡터 $\bf{w}$의 선형 결합으로 결정 함수 $\phi(z)$를 정의한다. 최종 입력은 $z = w_1x_1 + \cdots w_mx_m$이다.

 

특정 샘플 $x^{(i)}$의 최종 입력이 사전에 정의된 임계값 $\theta$보다 크면 클래스 1로 예측하고, 그렇지 않으면 클래스 -1로 예측한다. 퍼셉트론 알고리즘에서 결정 함수 $\phi(\cdot)$는 단위 계단 함수(unit step function)를 변형한 것이다.

$$\phi(z) = \begin{cases} 1 & {z \ge \theta}\\ -1 & \text{otherwise} \end{cases} $$

식을 간단하게 만들기 위해 임계값 $\theta$를 식의 왼쪽으로 옮겨 $w_0 = -\theta$이고 $x_0=1$인 0번째 가중치를 정의한다. 이렇게 하면 $z$를 조금 더 간단하게 쓸 수 있다.

$$z = \underbrace{w_0 x_0}_{-\theta} + w_1x_1 + \cdots + w_mx_m = \bf{w}^T \bf{x}$$

새로운 결정 함수는 다음과 같다.

$$\phi(z) = \begin{cases} 1 & {z \ge 0}\\ -1 & \text{otherwise} \end{cases} $$

 

---

2. 퍼셉트론 학습 규칙

1. 가중치를 0 또는 랜덤한 작은 값으로 초기화한다.

2. 각 훈련 샘플 $x^{(i)}$에서 다음 작업을 수행한다.

    a. 출력 값 $\hat{y}$를 계산한다.

    b. 가중치를 업데이트한다.

여기서 출력 값은 앞서 정의한 단위 계단 함수로 예측한 클래스 레이블이다. 가중치 벡터 $\bf{w}$에 있는 개별 가중치 $w_j$가 동시에 업데이트되는 것을 다음과 같이 쓸 수 있다.

$$w_j := w_j + \Delta w_j$$

가중치를 업데이트하는 데 사용되는 $\Delta w_j$값은 다음과 같은 규칙에 의해 계산된다.

$$\Delta w_j = \eta \left(y^{(i)} - \hat{y}^{(i)} \right)x_j^{(i)}$$

여기서 $\eta$는 학습률(Learning Rate)이라고 불리며, 일반적으로 0과 1 사이의 실수이다.

$y^{(i)}$는 $i$번째 훈련 샘플의 실제 클래스 레이블(True Class Label).

$\hat{y}^{(i)}$는 $i$번째 훈련 샘플의 예측 클래스 레이블(Predicted Class Label).

가중치 벡터의 모든 가중치를 동시에 업데이트 한다는 점이 중요하다. 즉 모든 가중치 $\Delta w_j$를 업데이트하기 전에 $\hat{y}^{(i)}$를 다시 계산하지 않는다. 구체적으로 2차원 데이터셋에서는 다음과 같이 업데이트 된다.

$$\Delta w_0 = \eta \left (y^{(i)}-output^{(i)} \right ) \\ \Delta w_1 = \eta \left ( y^{(i)}-output^{(i)} \right )x_1^{(i)} \\ \Delta w_2 = \eta \left(y^{(i)}-output^{(i)} \right)x_2^{(i)} $$

간단한 사고 실험을 해보자.

1. 퍼셉트론이 클래스를 레이블을 정확히 예측한 경우는 가중치가 변경되지 않고 그대로 유지된다.

$$\Delta w_j = \eta (-1--1)x_j^{(i)} = 0$$

$$\Delta w_j = \eta (1-1)x_j^{(i)} = 0$$

2. 잘못 예측했을 떄는 가중치를 양성 또는 음성 타깃 클래스 방향으로 이동한다.

$$\Delta w_j = \eta (1--1)x_j^{(i)} = \eta (2) x_j^{(i)}$$

$$\Delta w_j = \eta (-1-1)x_j^{(i)} = \eta (-2) x_j^{(i)}$$

곱셈 계수인 $x_j^{(i)}$를 좀 더 잘 이해하기 위해 다른 예를 살펴보자.

$$y^{(i)} = +1, \;\hat{y}_j^{(i)}=-1,\; \eta=1$$

$x_j^{(i)} = 0.5$일 때, 이 샘플을 -1로 잘못 분류했다고 가정하자. 이 때 가중치가 1만큼 증가되어 다음 번에 이 샘플을 만났을 때 최종 입력 $x_j^{(i)} \times w_j^{(i)}$가 더 큰 양수가 된다. 단위 계단 함수의 임계값보다 커져 샘플이 +1로 분류될 가능성이 높아질 것이다.

$$\Delta w_j^{(i)} = (1--1)0.5 = (2)0.5=1$$

가중치 업데이트는 $x_j^{(i)}$값에 비례한다. 예를 들어 $x_j^{(i)}=2$를 $1$로 잘못 분류했다면 이 샘플을 다음 번에 올바르게 분류하기 위해 더 크게 결정 경계를 움직인다.

$$\Delta w_j^{(i)} = (1--1)2 = (2)2=4$$

퍼셉트론은 두 클래스가 선형적으로 구분되고, 학습률이 충분히 작을 때만 수렴이 보장된다. 두 클래스를 선형 결정 경계로 나눌 수 없다면 훈련 데이터셋을 반복할 최대 횟수(에포크)를 지정하고 분류 허용오차를 지정할 수 있다. 그렇지 않으면 퍼셉트론은 가중치 업데이트를 멈추지 않는다.

 

---

3. 퍼셉트론 알고리즘 소스 코드 및 예제

Perceptron class 코드

class Perceptron(object):
    def __init__(self, eta=0.01, n_iter=50, random_state=1):
        self.eta = eta
        self.n_iter = n_iter
        self.random_state = random_state


    def fit(self, X, y):
        rgen = np.random.RandomState(self.random_state)
        self.w_ = rgen.normal(loc=0.0, scale=0.01, size=1 + X.shape[1])  # size = constant + features 
        self.errors_ = []
        for _ in range(self.n_iter):
            errors = 0
            for xi, target in zip(X, y):
                update = self.eta * (target - self.predict(xi))
                self.w_[1:] += update * xi
                self.w_[0] += update
                errors += int(update != 0.0)    # update가 0이 아니면 에러에 1을 더함
            self.errors_.append(errors)    # errors_ 리스트에 해당 iter의 errors값을 추가
        return self
    
    
    def net_input(self, X):
        return np.dot(X, self.w_[1:]) + self.w_[0]    # dot product 
    
    
    def predict(self, X):
        return np.where(self.net_input(X) >= 0.0, 1, -1)    # 최종 입력값이 0 이상이면 1, 아니면 -1

예제 데이터 & 산포도 그리기

# Example
import pandas as pd
df = pd.read_csv("https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data", header=None)
"""
seaborn을 이용할 경우.
import seaborn as sns
df = sns.load_dataset("iris")
"""

import matplotlib.pyplot as plt

# setosa와 versicolor 선택
y = df.iloc[0:100, 4].values    # label들로 이루어진 numpy.ndarray
y = np.where(y =='Iris-setosa', -1, 1)    # Iris-setosa의 label 은 -1, 아니라면 1

# 꽃받침 길이와 꽃잎 길이 추출
X = df.iloc[0:100, [0, 2]].values

plt.scatter(X[:50, 0], X[:50, 1], color='red', marker='o', label='setosa')
plt.scatter(X[50:100, 0], X[50:100, 1], color='blue', marker='x', label='versicolor')
plt.xlabel('sepal length[cm]')    # x축 이름 설정
plt.ylabel('petal length[cm]')    # y축 이름 설정
plt.legend(loc='upper left')      # 범례 위치: 좌상단
plt.show()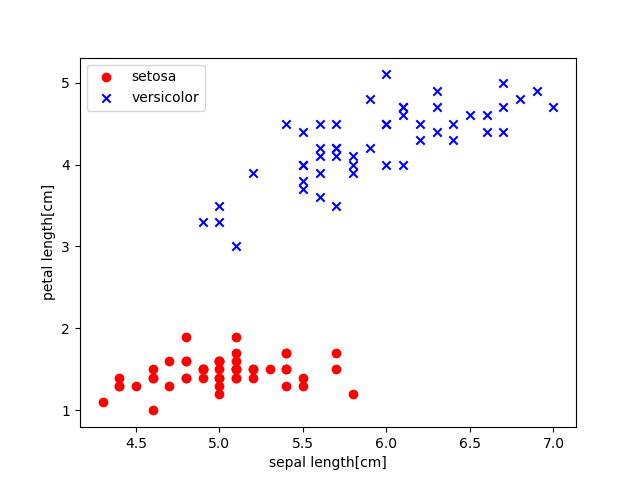

모델 학습시키기

# 에포크 대비 오차
ppn = Perceptron(eta=0.1, n_iter=10)    # iteration: 10
ppn.fit(X, y)    # implement fitting procedure
plt.plot(range(1, len(ppn.errors_) + 1), ppn.errors_, marker='o')
plt.xlabel('Epochs')
plt.ylabel('Number of Errors')
plt.show()

 

# 결정경계 시각화
from matplotlib.colors import  ListedColormap

def plot_decision_regions(X, y, classifier, resoultion=0.02):

    # 마커와 컬러맵 설정
    markers = ('o', 'x', 's', '^', 'v')
    colors = ('red', 'blue', 'lightgreen', 'gray', 'cyan')
    cmap = ListedColormap(colors[:len(np.unique(y))])

    # 결정 경계 그리기
    x1_min, x1_max = X[:, 0].min() - 1, X[: , 0].max() + 1
    x2_min, x2_max = X[ :, 1].min( ) - 1, X[ :, 1].max( ) + 1
    xx1, xx2 = np.meshgrid(np.arange(x1_min, x1_max, resolution),
			   				np.arange(x2_min, x2_max, resolution))
    Z = classifier.predict(np.array([xx1.ravel(), xx2.ravel()]).T)
    Z = Z.reshape(xx1.shape)
    plt.contourf(xx1, xx2, Z, alpha=0.3, cmap=cmap)
    plt.xlim(xx1.min(), xx1.max())
    plt.ylim(xx2.min(), xx2.max())

    # 산점도 그리기
    for idx, cl in enumerate(np.unique(y)):
        plt.scatter(x=X[y == cl, 0 ],
                    y=X[y==cl, 1],
                    alpha=0.8,
                    c=colors[idx],
                    markers=markers[idx],
                    label=cl,
                    edgecolor='black')

plot_decision_regions(X, y, classifier=ppn)
plt.xlabel('sepal length [cm]')
plt.ylabel('petal length [cm]')
plt.legend(loc='upper left')
plt.show()