Adative Linear Neuron(적응형 선형 뉴런; Adaline)

Intro

Adaline(이하 아달린)은 퍼셉트론의 향상된 버전으로 볼 수 있다. 아달린은 연속 함수를 비용함수로 정의하고 최소화한다. 아달린 규칙(위드로우-호프 규칙)과 로젠블라트의 퍼셉트론의 가장 큰 차이점은 가중치를 업데이트하는 데 퍼셉트론처럼 단위 계단 함수 대신 선형 활성화 함수를 사용한다는 점이다. 아달린에서 선형활성화 함수 $\phi(z)$는 최종 입력과 동일한 함수이다. 즉 다음과 같다.

$$\phi(\mathbf w^T \mathbf x) = \mathbf w^T \mathbf x$$

선형 활성화 함수가 가중치 학습에 사용되지만 최종 예측을 만드는 데에는 여전히 임계함수를 사용한다. 퍼셉트론에서의 단위 계단 함수와 유사하다. 아달린 알고리즘은 진짜 클래스 레이블과 선형 활성화 함수의 실수 출력값을 비교하여 모델의 오차를 계산하고 가중치를 업데이트한다. 반대로 퍼셉트론은 진짜 클래스 레이블과 예측 클래스 레이블을 비교한다.

Gradient Descent

미적분학에서, 어떤 점에서의 Gradient란 그 점에서 기울기가 가장 빠르게 증가하는 방향을 나타내는 벡터이며 원소는 각각의 변수에 대한 편미분계수이다. 따라서 Gradient Descent는 어떤 점에서의 gradient의 반대 방향으로 나아가 극솟값에 도달하는 방법이다. (방법론적으로는 수리통계에서 배운 Newton-Raphson Method와 유사한 것 같다.)

 

지도 학습 알고리즘의 핵심 구성요소는 학습 과정 동안 최적화하기 위해 정의한 목적함수이다. 종종 최소화하려는 비용함수가 목적 함수가 된다. 아달린은 계산된 출력과 진짜 클래스 레이블 사이의 제곱 오차합으로 가중치를 학습할 비용함수를 정의한다.

$$J(\mathbf{w}) = \frac{1}{2} \sum_i \left( y^{(i)}-\phi(z^{(i)} ) \right)$$

단위 계단 함수 대신 연속적인 선형 활성화 함수를 사용하는 장점은 비용 함수가 미분가능해진다는 점이다. 이 비용 함수의 또 다른 장점은 볼록함수라는 점이다.

$$\mathbf{w}:= \mathbf{w}+\Delta \mathbf{w}$$

$$\Delta \mathbf{w} = -\eta \nabla J(w)$$

$$\frac{\partial J}{\partial w_j} = - \sum_{i=1}\left(y^{(i)} - \phi(z^{(i)}) \right)x_j^{(i)}$$

퍼셉트론과 달리 아달린의 $\phi(z^{(i)})$는 정수 클래스 레이블이 아닌 실수임에 다시 한번 주의하자. 또 훈련 세트에 있는 모든 샘플을 기반으로 가중치를 업데이트하며 각 샘플마다 가중치를 업데이트 하지는 않는다. (퍼셉트론에서는 각 샘플마다 업데이트)따라서 이러한 방식을 Batch Gradient Descent (배치 경사 하강법)이라고도 한다.

Source Code

""" Adaline (ADAptive LInear NEuron, 적응형 선형 뉴런)
: use a linear activation function instead of a unit step function as in the Perceptron when updating the weights.
 가중치를 업데이트하는 데 퍼셉트론처럼 단위 계단 함수가 아닌 선형활성화 함수를 사용."""

# 1. Minimizing the cost function using GRADIENT DESCENT; 경사 하강법으로 비용 함수 최소화
# cost function  J(w) = (1/2) * sigma{y_(i) -phi(z_(i))}^2

import numpy as np
import matplotlib.pyplot as plt

class AdalineGD(object):
    """ Adaptive linear neuron  classifier

     parameter              # 임의로 설정
     -----------
     eta : float
        learning rate is a float between 0 and 1.
     n_iter : int
        the number of training data set repetition.
     random_state : int
        random number creating seed for weight random initialization.

     attribute
     ----------
     w_ : 1d-array          # 학습된 가중치 행렬 : 1차원 벡터
        trained weight
     cost_ : list            # epoch 마다 누적된 classification error
        the squared sum of cost function accumulated by each epoch

    """
    def __init__(self, eta=0.01, n_iter=50, random_state=1):
        self.eta = eta
        self.n_iter = n_iter
        self.random_state = random_state

    def fit(self, X, y):
        """ Learning a training data

        parameter
        --------------
        X : {array-like}, shape = [n_samples, n_features]
            a training data consisting of n_samples number of samples and n_features number of features.
        y : array-like, shape = [n_samples]
            target value

        return
        ---------
        self : object

        """
        rgen = np.random.RandomState(self.random_state)
        self.w_ = rgen .normal(loc=0.0, scale=0.01, size=1 + X.shape[1])
        self.cost_ = []

        for i in range(self.n_iter):
            net_input = self.net_input(X)
            output = self.activation(net_input)
            errors = y - output
            self.w_[1:] += self.eta * X.T.dot(errors)
            self.w_[0] += self.eta * errors.sum()
            cost = (errors  ** 2).sum() / 2.0
            self.cost_.append(cost)
        return self

    def net_input(self, X):
        """final input calculation"""
        return np.dot(X, self.w_[1:]) + self.w_[0]

    def activation(self, X):
        """calculate a linear activation"""
        return X

    def predict(self, X):
        """return class labels using a step function."""
        return np.where(self.activation(self.net_input(X)) >= 0.0, 1, -1)

# perceptron처럼 개별 훈련 샘플마다 평가한 후 weight를 업데이트하는 것이 아니라, 전체 training dataset을 기반으로 Gradient 계산.

Dataset

import pandas as pd
df = pd.read_csv('https://archive.ics.uci.edu/ml/'
                  'machine-learning-databases/iris/iris.data',
                  header = None)
df.tail()     # check

import matplotlib.pyplot as plt

# setosa와 versicolor 선택
y = df.iloc[0:100, 4].values    # label
y = np.where(y =='Iris-setosa', -1, 1)    # Iris-setosa의 label 은 -1, 아니라면 1

# 꽃받침 길이와 꽃잎 길이 추출
X = df.iloc[0:100, [0, 2]].values

Visualization

import matplotlib.pyplot as plt

# choose setosa and versicolor
y = df.iloc[0:100, 4].values
y = np.where(y == 'Iris-setosa', -1, 1)

# extracting lengths of sepal length(0) and petal length(2)
X = df.iloc[0:100, [0, 2]].values

fig, ax = plt.subplots(nrows=1, ncols=2, figsize=(10, 4))

ada1 = AdalineGD(n_iter=10, eta=0.01).fit(X, y)
ax[0].plot(range(1, len(ada1.cost_) + 1), np.log10(ada1.cost_), marker='o')
ax[0].set_xlabel('Epochs')
ax[0].set_ylabel('log(Sum-squared-error)')
ax[0].set_title('Adaline - Learning rate 0.01')

ada2 = AdalineGD(n_iter=10, eta=0.0001).fit(X, y)
ax[1].plot(range(1, len(ada2.cost_) + 1), ada2.cost_, marker='o')
ax[1].set_xlabel('Epochs')
ax[1].set_ylabel('Sum-squared-error')
ax[1].set_title('Adaline - Learning rate 0.0001')

plt.show()

"""
<Left Panel> 
: Since it has too high learning rate, it passes the global minimum value. 

<Right Panel>
: Since it has too high learning rate, it takes many epochs to approach to the global minimum value. 
"""

이 경우 학습률이 너무 크기 때문에 전역 최솟값으로 수렴하지 못한다.

---

 

Improving gradient descent through feature scaling

$\mathbf x_j$: j번째 특성 벡터

$$\mathbf x_j = \frac{\mathbf x_j - \mu_j}{\sigma_j}$$

표준화가 경사 하강법 학습에 도움이 되는 이유 중 하나는 더 적은 단계를 거쳐 최적 혹은 좋은 솔루션을 찾기 때문이다.

 

---

Large-scale Machine Learning and Stochastic Gradient Descent

데이터 셋이 매우 큰 경우, 배치 경사 하강법을 실행하면 계산 비용이 매우 많이 든다. 전역 최솟값으로 나아가는 단계마다 매번 전체 훈련 데이터셋을 다시 평가해야 하기 때문이다. 이에 대한 대안으로서 Stochastic Gradient Descent(확률적 경사 하강법)을 사용한다. 모든 샘플에 대하여 누적된 오차의 합을 기반으로 가중치를 업데이트 하는 대신, 각 훈련 샘플에 대해서 조금씩 가중치를 업데이트한다. 식은 아래와 같다.(summation이 빠졌음에 주목)

$$\nabla \mathbf w = \eta \left( y^{(i)} - \phi (z^{(i)}) \right ) \mathbf x^{(i)}$$

가중치가 더 자주 업데이트되기 때문에 수렴 속도가 훨씬 빠르다. 확률적 경사 하강법에서 만족스러운 결과를 얻으려면 훈련 샘플 순서를 무작위하게 주입하는 것이 중요하다. 또 순환되지 않도록 에포크마다 훈련 세트를 섞는 것이 좋다.

• 고정된 학습률 $\eta$를 시간이 지남에 따라 적응적인 학습률로 대체

  $$\frac{c_1}{\text{number of iteration}+c_2}$$

확률적 경사 하강법의 또 다른 장점은 온라인 학습으로 사용할 수 있다는 점.

온라인 학습에서 모델은 새로운 훈련 데이터가 도착하는 대로 훈련된다. 많은 양의 훈련 데이터가 있을 때도 유용.

• Mini Batch Learning

  배치 경사 하강법과 확률적 경사 하강법 사이의 절충점. 훈련 데이터의 작은 일부분으로 배치 경사 하강법을 적용하는 것. 배치 경사 하강법에 비해 장점은 가중치 업데이트가 더 자주 일어나므로 수렴속도가 더 빠르다. 또 확률적 경사 하강법에서 훈련 샘플을 순회하는 for문을 벡터화된 연산으로 바꾸어주므로 계산 효율성이 크게 상승한다.

Source Code

import numpy as np

class AdalineSGD(object):
    def __init__(self, eta=0.01, n_iter=10, shuffle=True, random_state=None):
        self.eta = eta
        self.n_iter = n_iter
        self.w_initialized = False
        self.shuffle = shuffle
        self.random_state = random_state

    def fit(self, X, y):
        self._initialize_weights(X.shape[1])
        self.cost_ = []
        for i in range(self.n_iter):
            if self._shuffle:
                X, y = self._shuffle(X, y)
            cost = []
            for xi, target in zip(X, y):
                cost.append(self._update_weights(xi, target))
            avg_cost = sum(cost) / len(y)
            self.cost_.append(avg_cost)
        return self

    def partial_fit(self, X, y):
        if not self.w_initialized:
            self._initialize_weights(X.shape[1])
        if y.ravel().shape[0] > 1:
            for xi, target in zip(X, y):
                self._update_weights(xi, target)
        else:
            self._update_weights(X, y)
        return self

    def _shuffle(self, X, y):
        r = self.rgen.permutation(len(y))
        return X[r], y[r]

    def _initialize_weights(self, m):
        self.rgen = np.random.RandomState(self.random_state)
        self.w_ = self.rgen.normal(loc=0.0, scale=0.01, size=1 + m)
        self.w_initialized = True

    def _update_weights(self, xi, target):
        output = self.activation(self.net_input(xi))
        error = target - output
        self.w_[1:] += self.eta * xi.dot(error)
        self.w_[0] += self.eta * error
        cost = 0.5 * error**2
        return cost

    def net_input(self, X):
        return np.dot(X, self.w_[1:]) + self.w_[0]

    def activation(self, X):
        return X

    def predict(self, X):
        return np.where(self.activation(self.net_input(X)) >= 0.0, 1, -1)

• np.random.RandomState.permutation(n) : 0부터 n-1 까지 n 개의 숫자를 랜덤한 숫자 시퀀스 생성

Visualization

X_std = np.copy(X)
X_std[: , 0] = (X[:, 0] - X[: ,0].mean()) / X[: ,0].std()
X_std[: , 1] = (X[:, 1] - X[: ,1].mean()) / X[: ,1].std()

ada = AdalineSGD(n_iter=20, eta=0.01, random_state=1)
ada.fit(X_std, y)

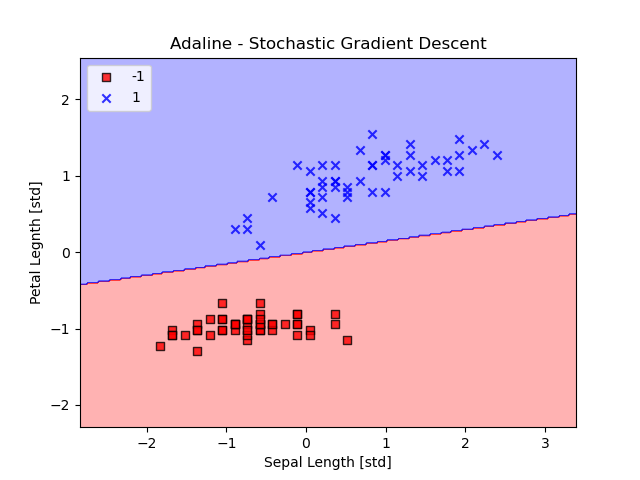
plot_decision_regions(X_std, y, classifier=ada)
plt.title("Adaline - Stochastic Gradient Descent")
plt.xlabel('Sepal Length [std]')
plt.ylabel('Petal Legnth [std]')
plt.legend(loc='upper left')
plt.show()

plt.plot(range(1, len(ada.cost_) + 1), ada.cost_, marker='o')
plt.xlabel('Epochs')
plt.ylabel('Average Cost')
plt.show()