statsmodels을 이용한 Ordinary Least Squares Regression

statsmodels을 이용하여 OLS 회귀를 실시하여 보자. 이하의 내용은 아래의 링크를 참고(사실상 번역)하였다. OLS Regression과 classical assumptions을 알고 있으면 이 글을 이해하는 데에 도움이 될 것이다.

Ordinary Least Squares — statsmodels

필요한 패키지 및 모듈을 불러오자.

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import statsmodels.api as sm

np.set_printoptions(precision=3)

np.random.seed(42)

1. OLS Estimation

100개의 무작위 표본을 생성하여 OLS 회귀를 실시해보자.

• 우선 $\mathbf{x}$를 0과 10 사이 100개의 값으로 설정한다.
• $\mathbf{X}$를 $\mathbf{x}$와 이를 제곱한 값들로 이루어진 $100 \times 2$ 행렬로 설정한다. 
• 계수를 $\pmb{\beta} = [1, 0.1, 10]^T$로 설정한다.
• 100개의 정규 무작위 오차로 이루어진 오차 벡터 $\mathbf{e}$를 생성한다.

nsample = 100
x = np.linspace(0, 10, 100)
X = np.column_stack((x, x**2))    # explanatory variables
beta = np.array([1, 0.1, 10])     # coefficient vector
e = np.random.normal(size=nsample)    # errors

statsmodel.api의 OLS regression에서 상수항을 포함한 회귀를 위해서는 상수항을 별도로 추가해주어야 한다. 상수항이 존재하지 않는 모델에서는 normal equation(정규방정식)의 첫 번째 식(오차항의 합이 0임)을 이용할 수 없다.  이렇게 상수항을 추가한 행렬을 다시 $X$로 설정하고, 이를 벡터 beta와 내적을 하여 무작위 오차 벡터 $e$를 더해준 벡터를 $y$로 설정한다.

X = sm.add_constant(X)
y = np.dot(X, beta) + e

식으로 표현하면 다음과 같다.

 

$$ y_n = \beta_0 + \beta_1 x_{n} + \beta_2 {x^2_{n}} + \epsilon_n$$

 

예를 들어, 50번째 표본에 대한 값들은 다음과 같다.

\begin{align}

X_{50} &=  [1, 5.05, 25.508] \\

y_{50} &=  X_{50} \mathbf{\beta}  + e_{50} \\

&= [1, 5.05, 25.508] \cdot [1, 0.1, 10] + 0.3241 \\

&= 256.9091

\end{align}

이제 $X$와 $y$에 대한 회귀분석을 할 준비를 마쳤다. model을 OLS로 설정하고 fitting하면 끝이다. 

model = sm.OLS(y, X)
result = model.fit()

OLS 회귀의 결과를 표로 확인하기 위하여 다음의 코드를 입력한다.

print(result.summary())

 

OLS 회귀 결과 요약

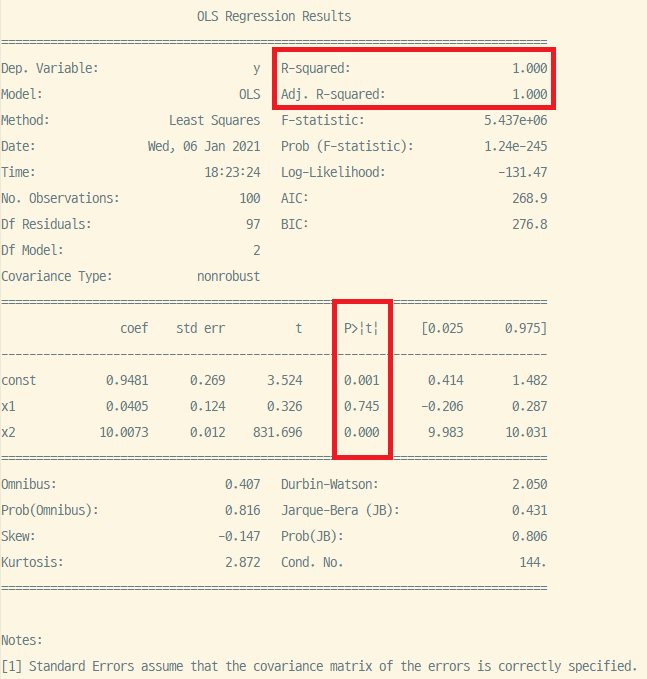
1. $R^2 = 1$. 설명변수가 독립변수 $y$의 변동을 완벽히 설명한다. 
2. $\beta_1 = 0.745$, $\beta_2=0$. $x_1$의 계수는 유의하지 않으나 $x_2$의 계수는 유의하다. 즉 $x_1$의 변동은 $y$의 변동을 적절하게 설명할 수 없다는 뜻이다. 혹시 이러한 상황이 일어난 원인을 모르겠다면 최초에 설정한 beta의 값들을 바꾸어서 회귀모형을 다시 돌려보기를 추천한다.

Skew(왜도), Kurtosis(첨도), DW(1차 자기상관 여부), JB(정규성 여부), Cond. No 등의 기타 계수는 일단은 무시하자. 만약 각 설명변수의 계수 및 $R^2$만을 알고 싶을 경우 아래의 코드를 입력하여 확인 가능하다.

print('Parameters: ', results.params)
print('R2: ', results.rsquared)

---

2. OLS non-linear curve but linear in parameters

이번엔 50개의 표본을 이용하여 조금 다르게 회귀를 실시하여 보자. 

nsample = 50
sig = 0.5
x = np.linspace(0, 20, nsample)  
X = np.column_stack((x, np.sin(x), (x-5)**2, np.ones(nsample)))   
beta = [0.5, 0.5, -0.02, 5.]

y_true = np.dot(X, beta)
y = y_true + sig * np.random.normal(size=nsample)    

res = sm.OLS(y, X).fit()
print(res.summary())

기본적인 변수 설정은 1의 틀에서 크게 벗어나지 않는다. $X$행렬이 $x$의 $sin$값, 이차함수, 1로 이루어졌을 뿐이다. 한편, 위에서 변수 y가 이제는 y_true로 설정되며, y는 y_true에 sig와 무작위 오차를 곱하여 더해준 값이다. 즉, y_true는 실제 독립변수이며 y는 관찰된 데이터라고 가정하고 회귀분석을 실시하는 셈이다. 

 

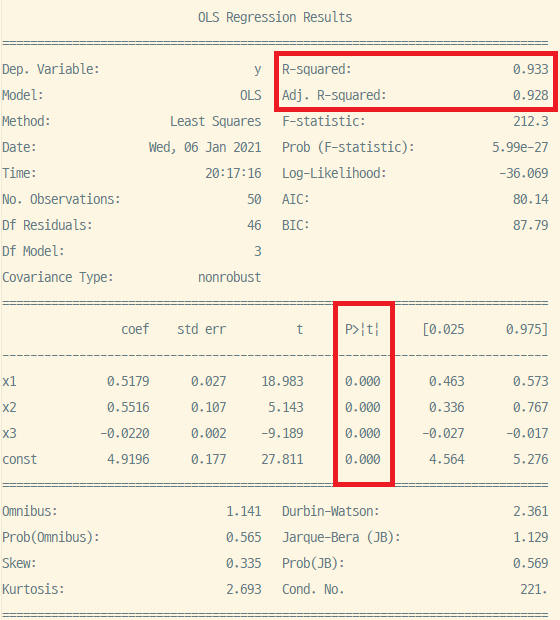
$R^2$는 1의 경우보다 소폭 하락했으나, 이번엔 모든 계수의 p-value가 0에 가깝고 따라서 모든 계수가 유의하다. 이제 신뢰구간을 간단하게 시각화해보자.

# Visualization
prstd, iv_l, iv_u = wls_prediction_std(res)

fig, ax = plt.subplots(figsize=(8, 6))

ax.plot(x, y, 'o', label="data")
ax.plot(x, y_true, 'b-', label="True")
ax.plot(x, res.fittedvalues, 'r--.', label="OLS")
ax.plot(x, iv_u, 'r--')
ax.plot(x, iv_l, 'r--')
ax.legend(loc='best');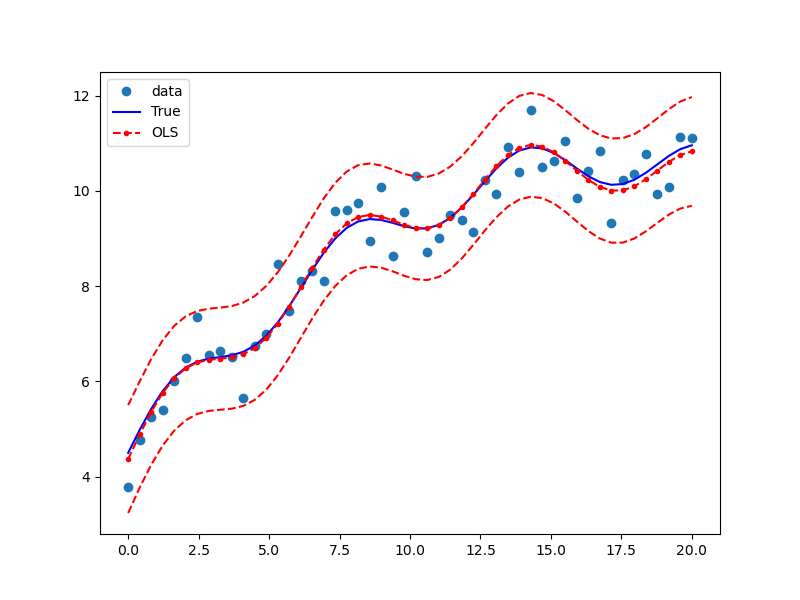

• 파란 점들은 관측된 데이터$(x, y)$를 나타낸다. 
• 가장자리의 빨간 점선은 OLS 회귀의 신뢰구간을 나타낸다.
• 가운데의 빨간 점선과 점은 OLS 회귀식과 표본의 fitted-value(각 X를 OLS 회귀식에 대입하여 도출한 값)를 나타낸다.
• 파란 실선은 실제 설명변수와 종속변수 간의 관계를 나타내며, 이는 OLS 회귀선과 유사하나 동일하지는 않다. 이를 반영한 것이 바로 $R^2 = 0.933$이다. 

 

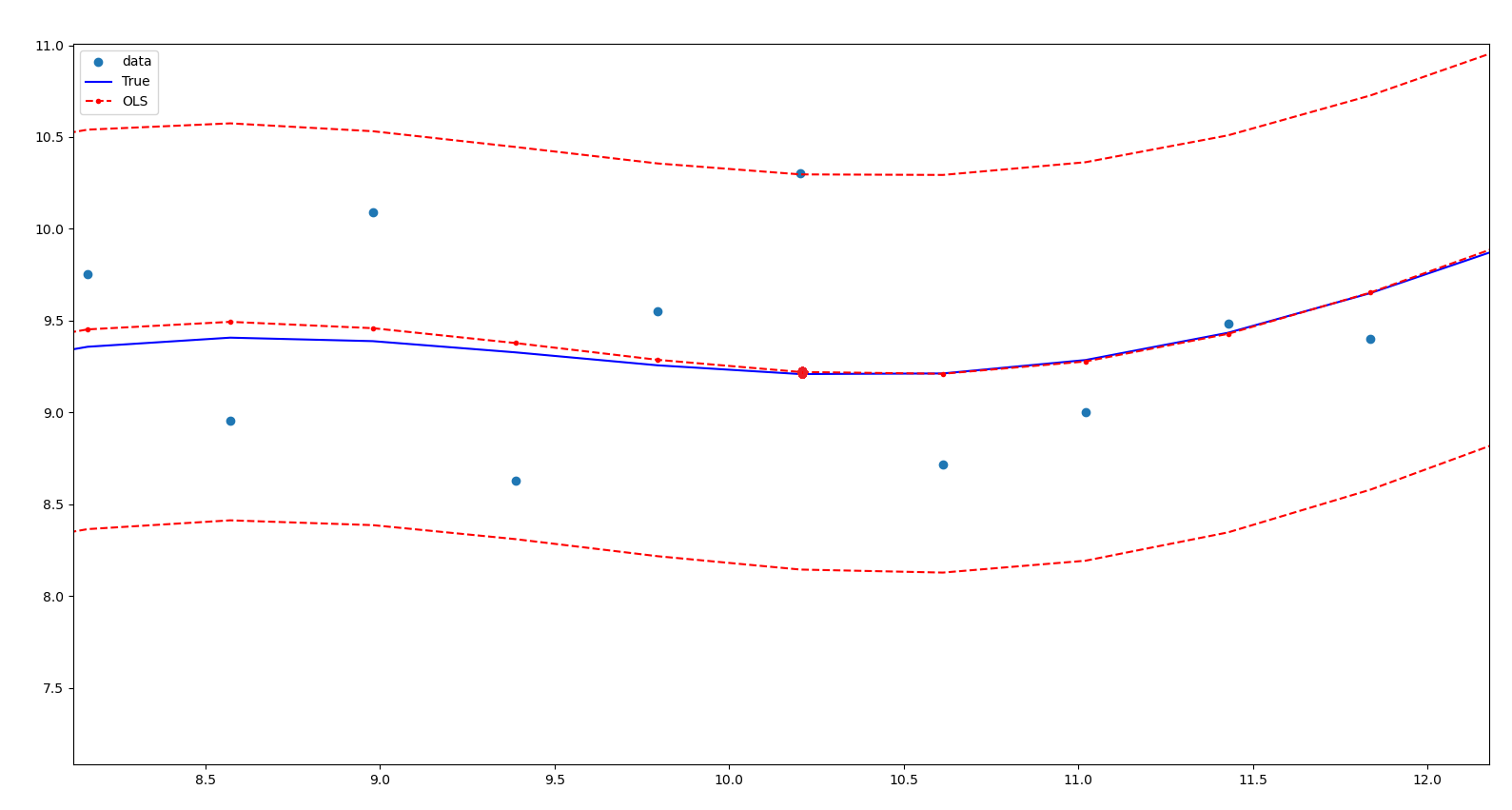
가령 25번째 표본을 살펴보면, $x_{25}=10.204, y_{25}= 10.304, y_{\text{true}}=9.209, y_{\text{prediction}}=9.22$이다. 즉, 실제값과 예측값이 크게 차이가 나지 않고 OLS회귀선이 $y_{\text{25, true}}$를 적절하게 예측하고 있다.

 

그림 가운데의 25번째 표본에 주목하자.